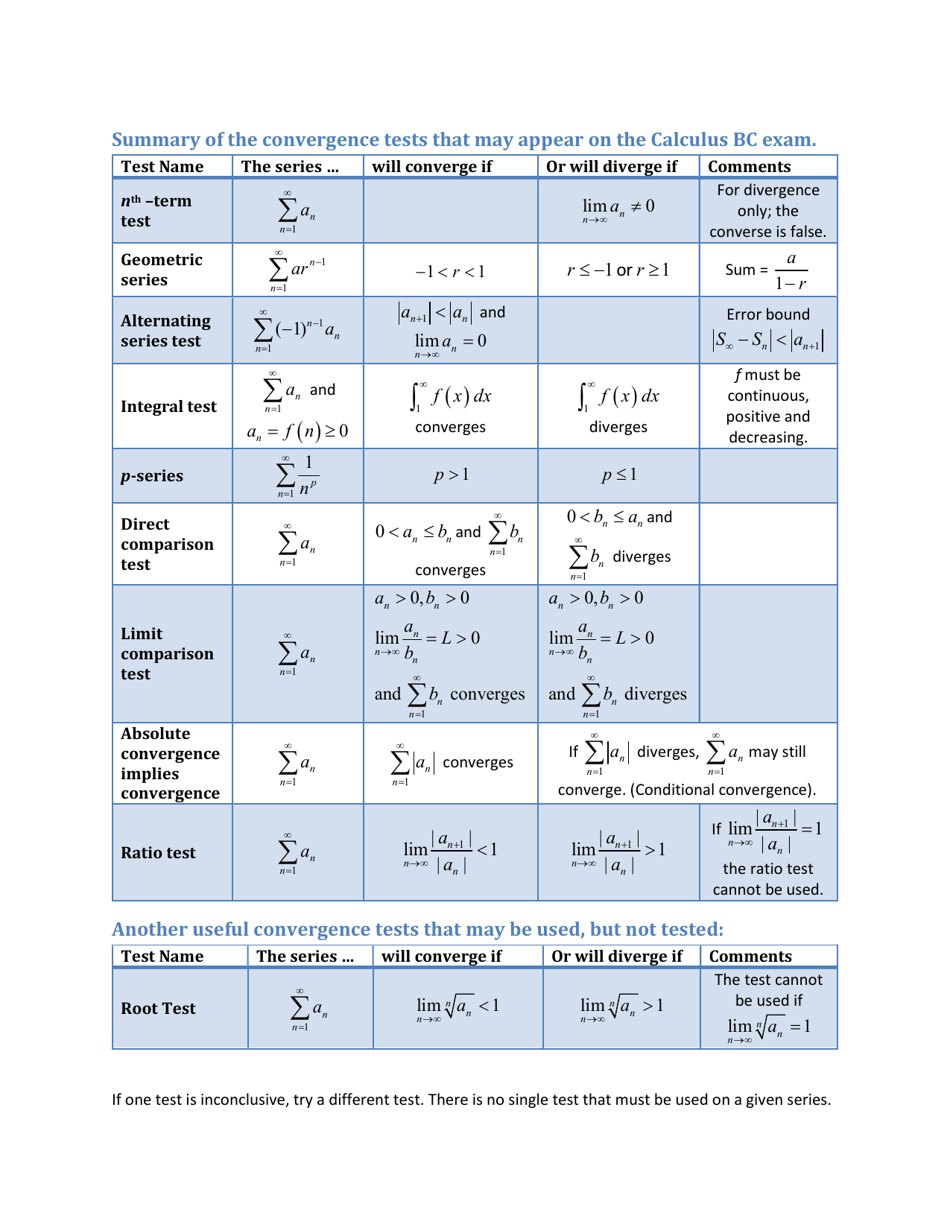
Calculus Series Cheat Sheet - 2 series cheat sheet theorem (alternating series test). If f(n) = sn, continuous, positive, decreasing: Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Let fb ngbe a sequence. P snconverges () r1 1. If all the terms snare positive. Then there exists a number c such that a < c < b and. If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow.
If f(n) = sn, continuous, positive, decreasing: P snconverges () r1 1. If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow. Then there exists a number c such that a < c < b and. Let fb ngbe a sequence. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). 2 series cheat sheet theorem (alternating series test). If all the terms snare positive.
If there exists some n such that for all n n (1) 0 < b n. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). 2 series cheat sheet theorem (alternating series test). This cheat sheet is not intended to be a list of guaranteed rules to follow. P snconverges () r1 1. If all the terms snare positive. Then there exists a number c such that a < c < b and. If f(n) = sn, continuous, positive, decreasing: Let fb ngbe a sequence.
Calculus Bc Exam Series Convergence Tests Cheat Sheet Download
If there exists some n such that for all n n (1) 0 < b n. If all the terms snare positive. Let fb ngbe a sequence. Then there exists a number c such that a < c < b and. This cheat sheet is not intended to be a list of guaranteed rules to follow.
Calculus II Cheat Sheet Series Download Printable PDF Templateroller
If f(n) = sn, continuous, positive, decreasing: P snconverges () r1 1. This cheat sheet is not intended to be a list of guaranteed rules to follow. Let fb ngbe a sequence. If there exists some n such that for all n n (1) 0 < b n.
Series Tests Cheat Sheet
If there exists some n such that for all n n (1) 0 < b n. If all the terms snare positive. If f(n) = sn, continuous, positive, decreasing: 2 series cheat sheet theorem (alternating series test). Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and.
Calculus 2 Cheat Sheet
If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow. If all the terms snare positive. If f(n) = sn, continuous, positive, decreasing: P snconverges () r1 1.
Calculus 2 Series And Sequences
P snconverges () r1 1. If all the terms snare positive. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). This cheat sheet is not intended to be a list of guaranteed rules to follow. If f(n) = sn, continuous, positive, decreasing:
Sequences and Series Cheat Sheet Download Printable PDF Templateroller
2 series cheat sheet theorem (alternating series test). This cheat sheet is not intended to be a list of guaranteed rules to follow. Let fb ngbe a sequence. If f(n) = sn, continuous, positive, decreasing: P snconverges () r1 1.
Calculus Cheat Sheet Formulas & Theorems
If there exists some n such that for all n n (1) 0 < b n. If all the terms snare positive. If f(n) = sn, continuous, positive, decreasing: Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). 2 series cheat sheet.
Calculus formula sheet Cheat Sheet Calculus Docsity
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). If there exists some n such that for all n n (1) 0 < b n. If f(n) = sn, continuous, positive, decreasing: Then there exists a number c such that a <.
Calculus 2 Cheat Sheet
Then there exists a number c such that a < c < b and. This cheat sheet is not intended to be a list of guaranteed rules to follow. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Let fb ngbe a.
Calculus 2 Cheat Sheet
Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). P snconverges () r1 1. 2 series cheat sheet theorem (alternating series test). Let fb ngbe a sequence. This cheat sheet is not intended to be a list of guaranteed rules to follow.
Then There Exists A Number C Such That A < C < B And.
2 series cheat sheet theorem (alternating series test). If all the terms snare positive. Suppose that f ( x ) is continuous on [a, b] and let m be any number between f ( a ) and f ( b ). Let fb ngbe a sequence.
P Snconverges () R1 1.
If f(n) = sn, continuous, positive, decreasing: If there exists some n such that for all n n (1) 0 < b n. This cheat sheet is not intended to be a list of guaranteed rules to follow.